You should test for interaction if you have two independent
variables that predict an outcome (dependent variable) and you suspect that
combining these variables will have an additional effect on the outcome. In other words, the relationship between X
and Y will be stronger, weaker or in the opposite direction at different values
of Z.
Example
To demonstrate, we will use data from a sample of 1,277
women of reproductive age in Thai Nguyen province. Stata software is used for
statistical analysis. We want to examine the relationship between women’s use
of modern contraceptive methods and the number of living children a woman
already has.
Research question: What
is the effect of having one additional child on the use of modern
contraceptives among women of reproductive age in Thai Nguyen province?
We
predict that the more children a woman has, the more likely she will be to use
modern contraception to prevent further pregnancies. However, we suspect that this
relationship varies according to women’s age. This is because both number of children
and age have been shown to predict contraceptive practices. In addition, younger
women and older women may have different attitudes and practices related to
both family size and contraceptive use.
To explore this relationship, we follow the steps below.
Descriptive statistics of the variables are provided below.
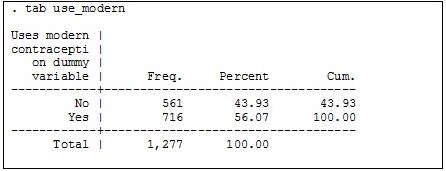
Dependent (Outcome) variable: Modern
contraceptive use [use_modern]
- No=0= Uses no contraception or uses traditional
contraceptive method
- Yes=1= Uses modern contraceptive method (IUD, condom, or
pill)
Independent
variables:
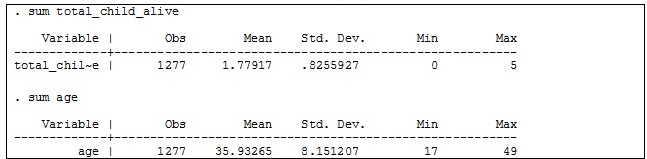
- Variable
of interest: Number of living children (continuous) [total_child_alive]
- Suspected
interaction or moderator variable: Age in years (continuous) [age]
Bivariate analysis
Using bivariate analysis, we can test the association
between the independent variables and modern contraceptive use. Because both of
the independent variables are continuous, we employ a t-test.
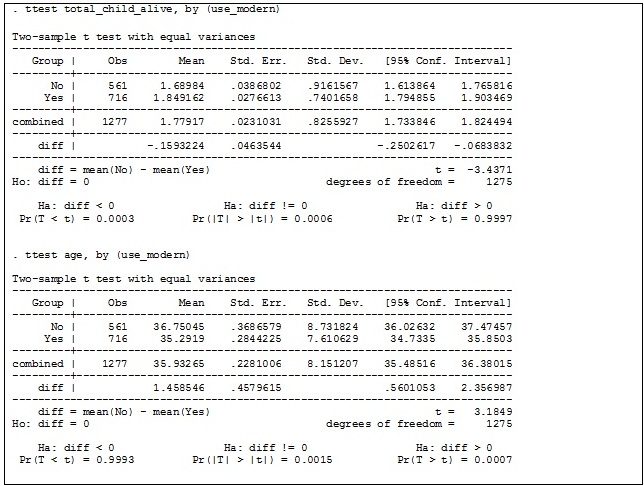
Both number of living children and
age are significantly associated with modern contraceptive use (P<0.01).
To
see if there is evidence of interaction, we examine the strength of the relationship
between the outcome and the independent variable of interest at different levels
of the third variable. In this example, we do so by using the logit command to
calculate the odds ratio (OR) for using modern contraception (yes vs. no) with
each additional child at different ages – 25 years, 35 years and 45 years.A) 25 years
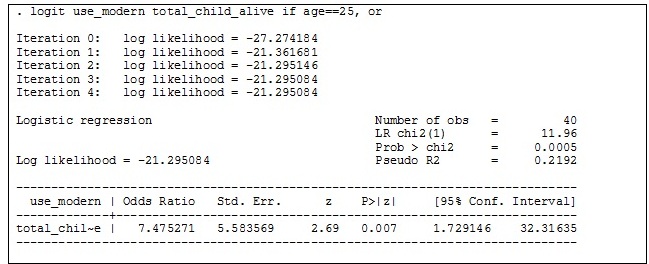
B) 35 years

C) 45 years
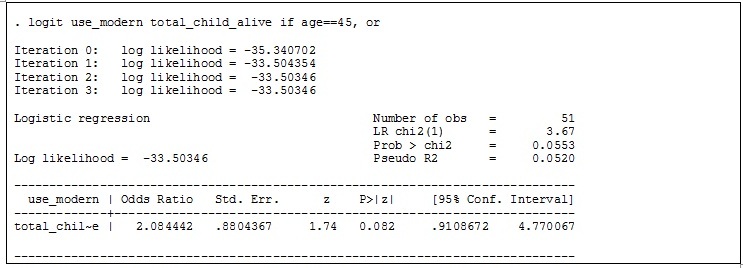
Results
suggest that there is an interaction since the relationship between modern
contraceptive use and number of living children is different among women aged
25 years (OR=7.48), 35 years (OR=1.00) and 45 years (OR=2.08).
Multivariate analysis
Now
we want to analyze how the relationship between modern contraceptive use and
number of living children is influenced by age. First, we fit a model with the
main effects of number of living children and age. Multiple logistic regression
is used because there is more than one independent variable with a binary
outcome (Note: the binary outcome should be coded as 0 and 1).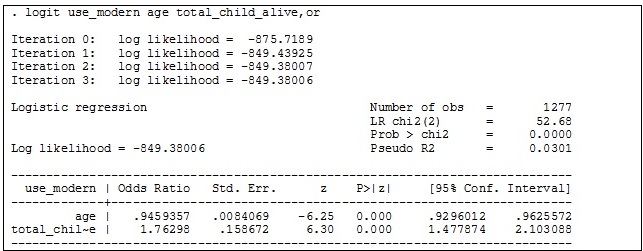
Findings show that the variable number of living children
is still significantly associated with modern contraceptive use, controlling
for age (P<0.001). You can also say that age is associated with modern
contraceptive use, controlling for number of living children (P<0.001). Having one additional child is associated with
1.76 times higher odds of using modern contraception with a 95% confidence
interval of 1.48-2.10.
Create an interaction
variable
The
most common approach for modeling interaction is to introduce a “cross-product”
interaction variable into the model. This variable is created by multiplying
the two independent variables. In this case, we create the interaction variable
by multiplying number of living children and age.
Fit the model with
the interaction variable
After
creating the interaction variable, we add it to the model.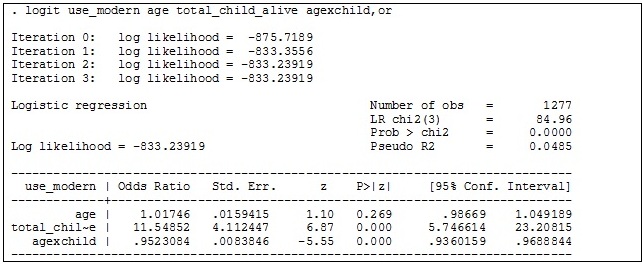
Wald test
Use
the Wald test to confirm that the interaction term is significant in the model.
The
interaction term is statistically significant (P<0.001), which means that
the relationship between modern contraceptive use and number of living children
depends on women’s age.
Obtain the odds
ratios
We
now know that there is an association between modern contraceptive use and
number of living children and that this association varies by age. To measure
the magnitude of this association, we estimate the ORs for women of different
ages. The lincom command is used to generate the OR and 95% confidence interval
(CI).A) Comparing two women aged 25 years – one woman
has 1 more child than the other
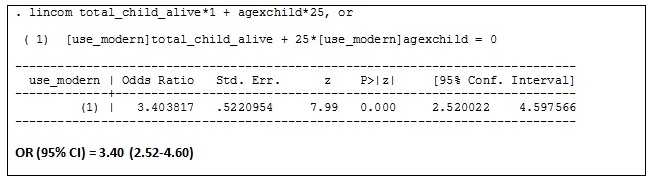
Note: Because age is
the same for both women, it is held constant. This means that you do not need
to include the variable “age” in the equation for the lincom command. Only the variables that differ between the
respondents you are comparing should be included.
B) Comparing
two women aged 35 years – one woman has 1 more child than the other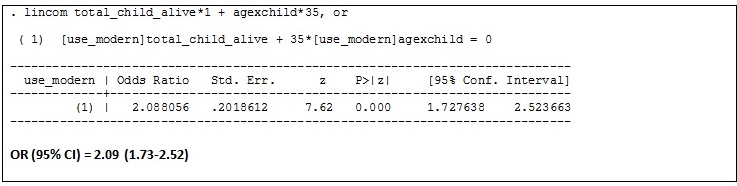
C) Comparing two women aged 45 years – one woman
has 1 more child than the other

Conclusion
The
association between number of living children and modern contraceptive use
depends on age. As age increases, the relationship between modern contraceptive
use and number of children diminishes. Among
women aged 25 years, having one additional child is associated with 3.40 times
increased odds of using modern contraception. By comparison, women aged 45
years with one additional child have only 1.28 greater odds of using modern
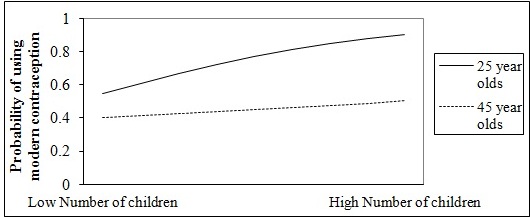
contraceptives compared to their counterparts with fewer children. This is also
seen in the graph below. The slope is steeper for 25 year olds than 45 year
olds, indicating that the relationship between number of children and modern
contraception use is stronger in this age group.
Sarah Keithly - Thongke.info

